Hash Tables 101

Vermutlich jeder Software Entwickler hat schon mal eine Hashtabelle (oder auch Hash Map) genutzt. Diese extrem hilfreiche Datenstruktur erlaubt es, Schlüssel-Wert-Paare effizient (konstanter Zeitaufwand, O(1)) zu speichern und wiederzufinden. Doch wie funktioniert eine Hashtabelle eigentlich genau, welche Möglichkeiten zur Implementierung gibt es und was gibt es zu beachten? Diesen Fragen wird im nachfolgenden Artikel auf den Grund gegangen. Wir werden versuchen eine simple Version einer Hashtabelle Stück für Stück konzeptionell zu erarbeiten.

Hashfunktionen

Integraler Bestandteil einer Hashtabelle ist eine sogenannte Hashfunktion. Vereinfacht ausgedrückt können wir mit einer Hashfunktion einen Eingabewert beliebiger Länge in einen Ausgabewert mit festgelegter Länge transformieren.

Weiterhin sollte eine Hashfunktion die Berechnung des Hashwerts möglichst effizient durchführen (kryptographische Hashfunktionen besitzen zusätzlich Eigenschaften, die unter anderem in Konflikt mit der effizienten Berechnung stehen, darauf gehen wir allerdings an dieser Stelle nicht weiter ein).

Zudem verteilt eine gute Hashfunktion die Eingabewerte möglichst gleichmäßig auf die Ausgabemenge. Das bedeutet, dass jeder Schlüssel („Selina“, „John“, „Edward“) mit der gleichen Wahrscheinlichkeit auf einen bestimmten Hashwert abgebildet wird. In diesem Zusammenhang sollten die Hashwerte auch so randomisiert sein, dass eine geringe Änderung des Schlüssels einen vollkommen unterschiedlichen Hashwert ergibt. Das verhindert, dass ähnliche Schlüssel Hashwerte mit einem bestimmten Muster erzeugen.

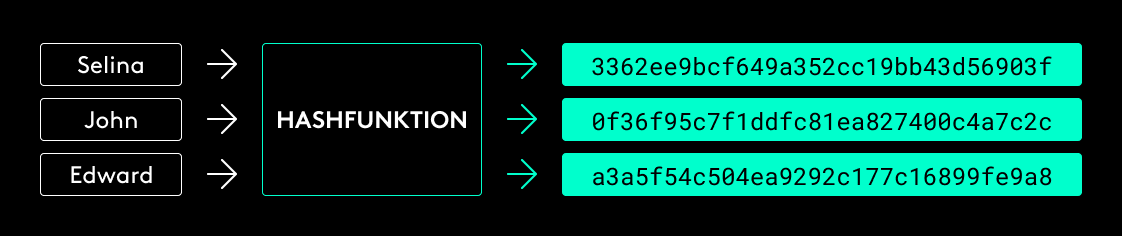
Wer gut aufgepasst hat, der hat sicherlich bemerkt, dass es vorkommen kann, dass zwei Eingabewerte auf den gleichen Hashwert abgebildet werden, da die mögliche Schlüsselmenge unbegrenzt, die Menge an möglichen Hashwerten durch die festgelegte Länge des Hashwerts begrenzt ist. Wir sprechen dann von einer Kollision. Durch die gleichmäßige Verteilung auf die möglichen Hashwerte, sollen Kollisionen möglichst geringgehalten werden, dennoch sind sie nicht gänzlich vermeidbar.

Interface

Für die weitere Betrachtung definieren wir zunächst ein simples Interface für unsere Hashtabelle:

Mit der put-Operation können wir einen Wert unter einem Schlüssel speichern und mit der get-Operation können wir den Wert mit diesem Schlüssel wiederfinden. Grundsätzlich ist es egal, was für Objekte wir als Schlüssel verwenden, solange wir einen Hashwert aus ihnen berechnen können.

Put

Für die put-Operation benötigen wir zunächst eine Datenstruktur, in der wir die Werte speichern können. Hierfür wird in der Regel ein Array genutzt, da ein Array sehr effizienten Zugriff (konstanter Zeitaufwand, O(1)) auf Werte über den entsprechenden Index bietet. Im Kontext von Hashtabellen werden die Positionen in diesem Array auch als (Hash-) Buckets bezeichnet. Daraus ergeben sich allerdings zwei Probleme:

• Wie kommen wir vom Schlüsselwert zu einem Integer-Index (Bucket) in unserem Array?

• Welche Größe hat das Array?

Schlüssel-Index-Mapping

Zunächst (wer hätte es gedacht) berechnen wir den Hashwert des Schlüssels. Je nach verwendeter Hashfunktion erhalten wir dann einen N-Bit Hashwert.

Für „normale“ Workloads würde uns bereits ein 32-Bit Integer mehr als genügen. Damit könnten wir 2^32 Buckets im Array adressieren. Liefert die Hashfunktion einen längeren Wert, können wir einfach die ersten 32 Bits verwenden und den Rest abschneiden. Anschließend müssen wir noch sicherstellen, dass der durch die Hashfunktion generierte Integer-Wert positiv ist (ein Array kann keine negativen Indexwerte haben). Dazu können wir einfach das Vorzeichen-Bit auf 0 setzen (da wir hier auf das Vorzeichen-Bit verzichten, können wir genau genommen „nur“ 2^31 Buckets adressieren).

Ein Beispiel in Pseudocode:

hash(“Selina”) => 3362ee9bcf649a352cc19bb43d56903f

takeFirst32Bit(3362ee9bcf649a352cc19bb43d56903f)
  => 11001101100010111011101001101111

// Jetzt wenden wir ein Bit-weises AND mit 0x7FFFFF an, um 
// sicherzustellen, dass das Vorzeichen-Bit positiv (0) wird:

11001101100010111011101001101111 &
01111111111111111111111111111111
  => 01001101100010111011101001101111

base10(01001101100010111011101001101111)
  => 1301002863

Somit würde der Schlüssel „Selina“ auf Bucket 1301002863 in unserem Array mappen. Wir können jetzt also beliebige Schlüssel über eine Hashfunktion auf Positionen in einem Array von 0 bis (2^31)-1 abbilden. Das ist schon mal nicht schlecht, allerdings würde das bedeuten, dass wir zunächst ein Array der Größe 2^31 erstellen müssten. Auf einem 64-Bit-System wären das 16GB RAM die dafür drauf gehen (vorausgesetzt wir speichern Zeiger).

Wie wir mit der Größe des Arrays umgehen, schauen wir uns später an. Für den Moment gehen wir davon aus, dass wir definitiv keine 1301002863 Positionen zur Verfügung haben, sondern beispielsweise 20. Um nun also zu unserem tatsächlichen Bucket zu gelangen wenden wir einfach den Modulo-Operator an:

Kollisionen

Dadurch, dass wir den Hashwert nochmals auf eine viel kleinere Wertemenge abbilden (nämlich die Positionen im Array), kommt es gelegentlich zu Kollisionen, zwei Schlüssel landen also im gleichen Bucket. Selbst wenn wir für jeden möglichen Hashwert einen Bucket im Array hätten, könnten wir Kollisionen nicht ausschließen.

Grundsätzlich gibt es zwei Optionen mit Kollisionen umzugehen:

• Offene Adressierung
  Wir können weitere (deterministische) Operationen auf den Index-Wert anwenden, bis wir bei einem freien Bucket im Array landen, oder wir wieder beim initialen (belegten) Bucket angekommen sind. In diesem Fall wäre unsere Hashtabelle voll und müsste vergrößert werden, dazu später mehr. Eine sehr simple Möglichkeit besteht darin, den Wert so lange um 1 zu inkrementieren, bis wir eine freie Stelle finden („lineares Sondieren“). Dabei müssen wir beachten, dass wir, sobald das Ende des Arrays erreicht ist, die Suche mit dem nächsten Inkrement an der ersten Position fortsetzen.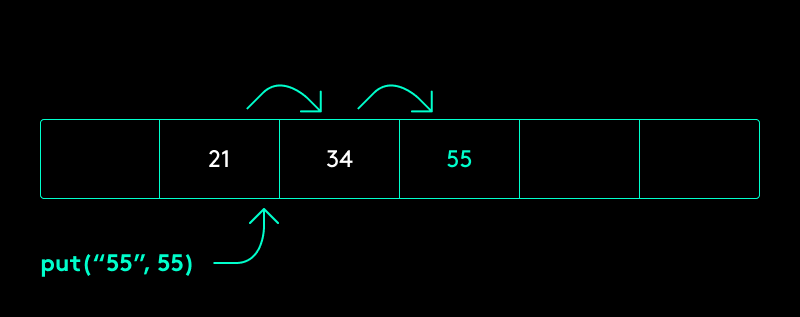

  

  Neben dem linearen Sondieren existieren weitere, teilw. effizientere Verfahren, wie bspw. quadratisches Sondieren, Doppel-Hashing oder Kuckucks-Hashing, auf die wir aber an dieser Stelle nicht weiter eingehen.

• Verkettung
  Anstatt die Werte direkt im Array zu speichern, können wir die Buckets so gestalten, dass diese jeweils aus einer weiteren dynamischen Datenstruktur bestehen. Dies kann z.B. eine verkettete Liste oder ein binärer Suchbaum sein. Wir fügen den Wert also nicht direkt in das Array ein, sondern in die entsprechende Datenstruktur, die sich hinter dem errechneten Bucket befindet.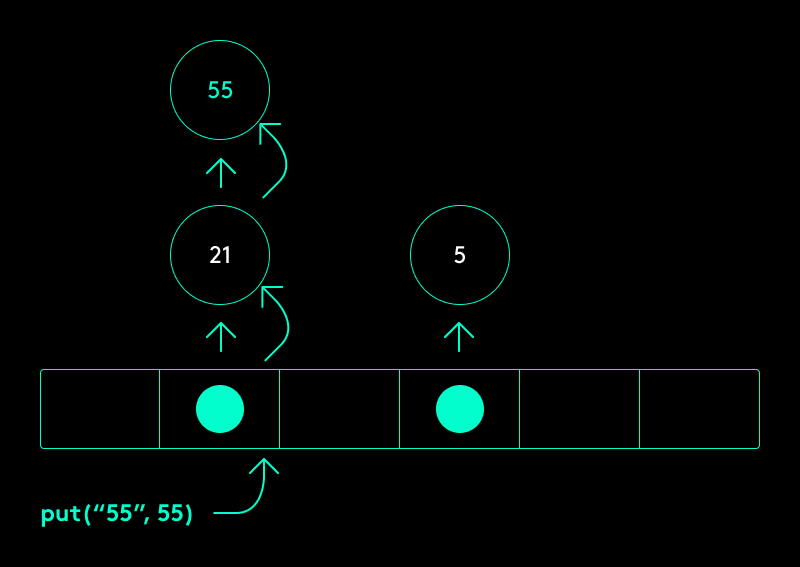

  

  Sowohl bei Verkettung als auch bei offener Adressierung muss zusätzlich zum Wert auch der Schlüssel gespeichert werden, um die Werte später wiederfinden zu können. Hätten wir nur den Schlüssel, könnten wir zwar bei einem Bucket landen, wüssten aber nicht welcher der richtige Wert in der darunterliegenden Datenstruktur (Verkettung) ist, oder ob wir den Index noch weiter inkrementieren müssen, um zum richtigen Bucket zu gelangen (offene Adressierung). Im Falle einer Kollision verschlechtert sich die Zugriffszeit auf O(1 + n), wobei n die Anzahl der Elemente im gleichen Bucket ist.

Array-Größe

Bei der Wahl der Größe des Arrays der Hashtabelle gibt es verschiedene Dinge zu beachten. Unter bestimmten Bedingungen ist es sinnvoll sicherzustellen, dass die Größe des Arrays einer Primzahl entspricht. Dies ist dann der Fall, wenn unsere Hashfunktion die Werte nicht ausreichend gleichmäßig verteilt, oder wir offene Adressierung zum Umgang mit Kollisionen nutzen. Im Kontext dieses Artikels beschäftigen wir uns mit diesen Fällen nicht weiter und nehmen an, dass unsere Hashfunktion gut ist und wir Verkettung nutzen, um mit Kollisionen umzugehen.

Anstelle einer Primzahl nutzen wir eine Zweierpotenz. Grundsätzlich könnten wir jede beliebige Zahl nehmen, eine Zweierpotenz hat nur einen Vorteil: Die Berechnung der Modulo-Operation kann sehr effizient über ein Bit-weises AND durchgeführt werden.

Eine wichtige Metrik für die Bestimmung der Größe des Arrays ist der sogenannte Ladungsfaktor (Load Factor). Er beschreibt wie „voll“ die Tabelle ist und berechnet sich wie folgt:

Häufig wird der Load Factor auch mit umgekehrtem Zähler und Nenner berechnet, also Größe / Elemente, dies ändert jedoch nichts an der Relation, die er beschreibt (nämlich den Füllgrad der Hashtabelle). Die folgende Hashtabelle hat beispielsweise einen Load Factor von ¾:

Überschreitet der Load Factor einen bestimmten Grenzwert, sollten wir unser Array vergrößern. Wir müssen an dieser Stelle einen Trade-Off zwischen Speicherverbrauch und Zugriffszeit machen. Je größer wir das Array im Vergleich zur Anzahl der gespeicherten Elemente halten, desto geringer ist die Wahrscheinlichkeit einer Kollision, allerdings belegen wir auch mehr Speicher. Als Faustregel wird häufig ein Load Factor von 3 bzw. 0,75 (je nach Berechnung) verwendet, da dieser einen guten Kompromiss zwischen Speicherverbrauch und Zugriffszeit bietet.

Sobald also jedes Bucket im Schnitt 3 Elemente enthält, sollten wir das Array vergrößern. Da wir uns für die Größe auf Zweierpotenzen beschränken, werden wir die Größe verdoppeln. Hierbei sollte natürlich beachtet werden, dass wir nicht bis ins unendliche Verdoppeln, sondern eine Maximalgröße definieren.

Weiterhin sollte erwähnt werde, dass die Vergrößerung eine relativ teure Operation ist. Dadurch, dass sich die Größe ändert, ändert sich auch die Zuweisung der Elemente auf die Buckets, da wir jetzt nicht mehr mod m, sondern mod 2m rechnen, um zu einem Bucket zu gelangen. Für alle Elemente muss also der Hash nochmal berechnet werden und sie müssen einem neuen Bucket zugewiesen werden. Wenn wir wissen, dass sich die Größe häufig verändern wird, kann zusätzlich zum Wert auch der Hash jedes Elements gespeichert werden, sodass wir nur die Modulo-Berechnung bei einer Vergrößerung durchführen müssen. Wenn wir die maximale Anzahl der Elemente kennen, können wir auch eine initiale Größe vorgeben, sodass wir niemals die teure Vergrößerungsoperation durchführen müssen. Andernfalls initialisieren wir unser Array mit einer „vernünftigen“ Standardgröße. Die HashMap-Klasse der Java-Standardbibliothek nimmt hierfür beispielsweise die Standardgröße 16.

Ganz so schlimm ist die Vergrößerung jedoch nicht. Obwohl es sich hierbei um einen sehr teuren Vorgang handelt, führen wir ihn nur bei jeder n^2-ten put-Operation aus. Somit amortisieren sich die Kosten für die Vergrößerung, wie bei einer Array-Liste, im Schnitt auf O(1). Mehr dazu hier.

Wir wissen jetzt also, wie wir Elemente in unsere Hashtabelle einsetzen:

1. Hash des Schlüssels berechnen

2. Bucket berechnen = Hashwert mod Arraygröße

3. In Bucket einfügen (entweder als erstes Element der verketteten Liste im Bucket oder ans Ende der Liste im Falle einer Kollision)

4. Load Factor und Grenzwert vergleichen und optional Vergrößerungsoperation durchführen

Get

Schließlich wollen wir auch auf die gespeicherten Elemente zugreifen. Dazu nutzen wir die get-Operation. Prinzipiell durchlaufen wir die gleichen Schritte wie bei insert:

1. Hash des Schlüssels berechnen

2. Bucket berechnen = Hashwert mod Arraygröße

3. Liste des Buckets iterieren und Schlüssel vergleichen

Schritte 1 und 2 benötigen einen konstanten Zeitaufwand. Schritt 3 ist der Flaschenhals, wenn es um die Performance geht. Je länger die Liste des Buckets ist, desto mehr Elemente müssen wir im Worst Case iterieren, bis wir zum Element mit dem gesuchten Schlüssel kommen. Aus diesem Grund begrenzen wir durch den Load Factor 3 (siehe oben) die Länge der Bucketlisten im Schnitt auf 3 Elemente. Dadurch benötigt die get-Operation durchschnittlich einen Zeitaufwand von O(1).

Fazit

Wie wir gesehen haben, steckt hinter einer vermeintlich simplen Hashtabelle doch einiges mehr an Komplexität als man vielleicht vermuten mag. Hier sind nochmal kurz die wichtigsten Erkenntnisse zusammengefasst:

• Die Performance einer Hashtabelle steigt und fällt mit den Kollisionen

• Kollisionen können reduziert werden durch:

  • Eine gute Hashfunktion / Nutzen einer Primzahl als Größe bei schlechter Hashfunktion

  • Vergrößern der Tabelle

• Über den Load Factor kann gesteuert werden, wie häufig eine Vergrößerung durchgeführt wird (Trade-Off: Speicherverbrauch vs. Performance)

• Performance für put & get:

  • Worst Case (nur Kollisionen, alle Elemente in einem Bucket): O(n)

  • Average Case (max. k Kollisionen pro Bucket, bestimmt durch Load Factor): O(1)

In der Regel empfiehlt es sich niemals eine solche Datenstruktur selbst zu implementieren, außer natürlich zu Übungszwecken ;)

Es gibt allerdings auch Ausnahmefälle wo eine eigene Implementierung sinnvoll sein kann, wenn ihr sehr spezielle Anforderungen oder Rahmenbedingungen habt.

Ich hoffe ich konnte euch mit diesem Artikel die ein oder andere neue Erkenntnis zu Hashtabellen geben. Ich habe jedenfalls während der Recherche einiges dazugelernt. Bis zum nächsten Mal!

MK